人生一世,誰(shuí)都不是順順利利的,誰(shuí)都會(huì)有犯錯(cuò)的時(shí)候,犯錯(cuò)是我們生命中必不可少的一部分。既然誰(shuí)都會(huì)犯錯(cuò),那人和人的區(qū)別就是對(duì)待錯(cuò)誤的態(tài)度。有些人是立馬尋找原因,改正錯(cuò)誤。有些人是任由錯(cuò)誤放在哪里,也不去解決,也不去尋找原因,吸收教訓(xùn)。對(duì)于前一種人來(lái)說(shuō),犯的錯(cuò)誤反而成為下一步成功的基礎(chǔ)。對(duì)于后一種人來(lái)說(shuō),往后的日子里,還會(huì)繼續(xù)犯同類(lèi)錯(cuò)誤,還會(huì)在同一個(gè)地方摔倒多次。
人生有三種跌倒:烏龜式跌倒,不倒翁式跌倒,和朝圣者式跌倒。烏龜式的跌倒就是一旦跌倒,就不再翻身,只是仰躺著眼瞪天空,等待外力來(lái)幫扶一把;
不倒翁式的跌倒就是總是不停地跌倒而且常常是在同一個(gè)地方,但每次都不屈地爬起,然后換個(gè)方向,繼續(xù)開(kāi)始下一輪的跌倒和爬起;而朝圣者式的跌倒,因?yàn)樾睦镉袀€(gè)堅(jiān)定的目標(biāo),比如去岡波仁齊峰朝圣,所以雖然跌倒了,但每次跌倒的地方也都更接近目標(biāo)。
愿我們每個(gè)人都能做朝圣者,讓每一次跌倒,都能讓我們更接近目標(biāo)。
1
應(yīng)用題中,我們經(jīng)常會(huì)列出一個(gè)方程,方程里面是一個(gè)未知數(shù),然后我們就能解出未知數(shù)的值。或者列出一個(gè)方程組,兩個(gè)未知數(shù)對(duì)應(yīng)兩個(gè)方程,三個(gè)未知數(shù)對(duì)應(yīng)三個(gè)方程,然后通過(guò)消元法,就能解出每一個(gè)未知數(shù)。這是我們常規(guī)的做應(yīng)用題的方法。
但是還有一類(lèi)題,其未知數(shù)的個(gè)數(shù)多于方程的個(gè)數(shù)。這類(lèi)問(wèn)題,我們一般稱(chēng)之為不定方程(組),不定方程(組)一般有無(wú)數(shù)組解,但題意往往要求我們求出其中的特殊解(一般為整數(shù)解)。對(duì)于這類(lèi)題,常規(guī)的解法就失去了作用,那怎么解決呢?我們常常利用整除、奇數(shù)偶數(shù)、范圍等特征來(lái)確定最后的答案。
先來(lái)一道題試試:
在年底的獻(xiàn)愛(ài)心活動(dòng)中,某單位共有100人參加捐款。經(jīng)統(tǒng)計(jì),捐款總額是19000元,個(gè)人捐款數(shù)額有100元、500元和2000元三種。該單位捐款500元的人數(shù)為()
A,13 B,18 C,25 D,30 E,38
我們的常規(guī)解法是設(shè)未知數(shù),然后列出方程:設(shè)捐款100元、500元和2000元的人數(shù)分別為x,y,z,則有下列方程: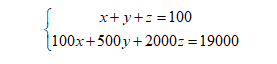
化簡(jiǎn)后:
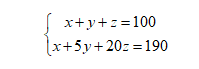
很明顯,兩個(gè)方程,三個(gè)未知數(shù),你要讓我通過(guò)消元法解出方程,我只能說(shuō):臣妾做不到啊!那怎么辦?走一步是一步,我先消掉一個(gè)未知數(shù)再說(shuō),兩個(gè)式子上下相減,得:
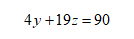
然后這個(gè)方程要想解出答案,是不太現(xiàn)實(shí)的,它有無(wú)數(shù)組解。可我們?cè)O(shè)的都是人數(shù),人數(shù)肯定是正整數(shù),那就好辦多了,我們一個(gè)個(gè)試也能試出來(lái)。我們分別讓z取1,2,3,4,5(為啥是這五個(gè)數(shù)呢,因?yàn)閦再大點(diǎn),y就得是負(fù)數(shù)啦),這里還有一個(gè)技巧,因?yàn)?y和90都是偶數(shù),所以19z也得是偶數(shù),所以z是偶數(shù),所以z取值就為2,4。通過(guò)驗(yàn)證,可得在z為2,y為13時(shí),為唯一的整數(shù)解組合。然后我們?cè)俅肭蟪鰔的值即可。
這是利用整數(shù)的一些性質(zhì)來(lái)解決這類(lèi)不定方程的一個(gè)案例,大家仔細(xì)琢磨琢磨哈!
2
上面是兩個(gè)方程,三個(gè)未知數(shù)讓我們求解的,就已經(jīng)夠我們頭疼的了,還有更狠的呢!一個(gè)方程,三個(gè)未知數(shù)!不過(guò),我們同樣能解,但是,得借助不等式的一些性質(zhì)。
下面看題:
在某次考試中,甲、乙、丙三個(gè)班得平均成績(jī)?yōu)?0,81,81.5,三個(gè)班得學(xué)生分?jǐn)?shù)之和為6952,三個(gè)班共有學(xué)生()
A,85 B,86 C,87 D,88 E,90
還是我們的常規(guī)思路,先設(shè)甲、乙、丙三個(gè)班的學(xué)生人數(shù)分別為x、y、z。那根據(jù)題意,我們列出方程:
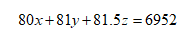
這,這,這,這讓我,獵人抓刺猬,無(wú)處下手啊!那這類(lèi)題如何做呢?這類(lèi)題沒(méi)有上面那道題的數(shù)字那么小,不適合用窮舉法解決。那這時(shí),我們就要利用不等式的一些性質(zhì),把要求解的東西的值給限制到一定的范圍,然后再計(jì)算。我們把式子變化一下。
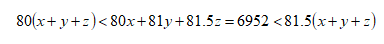
因?yàn)槲覀円蠼獾氖莤+y+z的值嘛,所以可以通過(guò)這個(gè)變化,給x+y+z計(jì)算出一個(gè)范圍,這個(gè)式子計(jì)算一下就是:
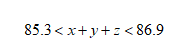
到這一步了,你還會(huì)說(shuō)不知道答案是啥么?
3
不定方程在我們的考試中出現(xiàn)的很少,但也差不多過(guò)幾年就有一個(gè),這類(lèi)題的特點(diǎn)就是看著很?chē)樔耍恢涝趺床拍芙獬龃鸢浮5忸}方法很容易掌握,說(shuō)破了就簡(jiǎn)單了。
下面我們看一種不定方程的另一種題型。
某單位年終共發(fā)了100萬(wàn)元獎(jiǎng)金,獎(jiǎng)金金額分別是一等獎(jiǎng)1.5萬(wàn)元、二等獎(jiǎng)1萬(wàn)元、三等獎(jiǎng)0.5萬(wàn)元。則該單位至少有100人。
(1)得二等獎(jiǎng)的人數(shù)最多。
(2)得三等獎(jiǎng)的人數(shù)最多。
這是一道條件充分性判斷題,是看哪個(gè)條件能推算出來(lái)該單位至少有100人。上面的兩道題,都是最終求解出一個(gè)整數(shù)的解。而這道題求的是一個(gè)范圍,怎么做呢,我們來(lái)做做看。
首先設(shè)領(lǐng)1.5萬(wàn)元,1萬(wàn)元,0.5萬(wàn)元的人數(shù)分別是x、y、z,(年終獎(jiǎng)夠豐厚得呀,老板,看這里,這里,我也要!)根據(jù)題意有:
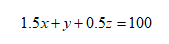
這個(gè)是題目中給的已知條件,最終就是看條件(1)和條件(2)哪個(gè)能推出來(lái)x+y+z≥100。我們來(lái)看條件(1),得二等獎(jiǎng)的人最多。條件(2),得三等獎(jiǎng)的人數(shù)最多。不管得二等獎(jiǎng)和三等獎(jiǎng)的人數(shù)是什么情況,我們的當(dāng)務(wù)之急就是建立上面的式子和x+y+z的關(guān)系,因?yàn)槲覀兊哪康木褪莤+y+z。那我們把上面的式子給變化一些,硬湊出一個(gè)x+y+z。
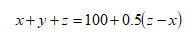
現(xiàn)在x+y+z湊出來(lái)了,而且尾巴上還帶了個(gè)100,好像和100有些關(guān)系了。既然要求最少100人,那么只要(z-x)≥0不就可以了嗎?即z≥x就可以了。我們看條件(1),只提到了y最大,和我們的推論沒(méi)關(guān)系,也推不出z≥x。條件(2)中,z最大,那z≥x是肯定成立的,因此這道題條件(1)不充分,條件(2)充分。選B。
好了,不定方程的內(nèi)容,我們就講到這里了,希望下期還能在這里遇見(jiàn)你,我們一起進(jìn)步、一起成長(zhǎng),迎接考試,迎接金榜題名的那一天!




